---

8.36 contour ¶

This module draws contour lines. To construct contours corresponding to the values in a real array c for a function f on box(a,b), use the routine

guide[][] contour(real f(real, real), pair a, pair b,
                  real[] c, int nx=ngraph, int ny=nx,
                  interpolate join=operator --, int subsample=1);

The integers nx and ny define the resolution. The default resolution, ngraph x ngraph (here ngraph defaults to 100) can be increased for greater accuracy. The default interpolation operator is operator -- (linear). Spline interpolation (operator ..) may produce smoother contours but it can also lead to overshooting. The subsample parameter indicates the number of interior points that should be used to sample contours within each 1 x 1 box; the default value of 1 is usually sufficient.

To construct contours for an array of data values on a uniform two-dimensional lattice on box(a,b), use

guide[][] contour(real[][] f, pair a, pair b, real[] c,
                  interpolate join=operator --, int subsample=1);

To construct contours for an array of data values on a nonoverlapping regular mesh specified by the two-dimensional array z,

guide[][] contour(pair[][] z, real[][] f, real[] c,
                  interpolate join=operator --, int subsample=1);

To construct contours for an array of values f specified at irregularly positioned points z, use the routine

guide[][] contour(pair[] z, real[] f, real[] c, interpolate join=operator --);

The contours themselves can be drawn with one of the routines

void draw(picture pic=currentpicture, Label[] L=new Label[],
          guide[][] g, pen p=currentpen);

void draw(picture pic=currentpicture, Label[] L=new Label[],
          guide[][] g, pen[] p);

The following simple example draws the contour at value 1 for the function z=x^2+y^2, which is a unit circle:

import contour;
size(75);

real f(real a, real b) {return a^2+b^2;}
draw(contour(f,(-1,-1),(1,1),new real[] {1}));

The next example draws and labels multiple contours for the function z=x^2-y^2 with the resolution 100 x 100, using a dashed pen for negative contours and a solid pen for positive (and zero) contours:

import contour;

size(200);

real f(real x, real y) {return x^2-y^2;}
int n=10;
real[] c=new real[n];
for(int i=0; i < n; ++i) c[i]=(i-n/2)/n;

pen[] p=sequence(new pen(int i) {
    return (c[i] >= 0 ? solid : dashed)+fontsize(6pt);
  },c.length);

Label[] Labels=sequence(new Label(int i) {
    return Label(c[i] != 0 ? (string) c[i] : "",Relative(unitrand()),(0,0),
                 UnFill(1bp));
  },c.length);

draw(Labels,contour(f,(-1,-1),(1,1),c),p);

The next examples illustrates how contour lines can be drawn on color density images, with and without palette quantization:

import graph;
import palette;
import contour;

size(10cm,10cm);

pair a=(0,0);
pair b=(2pi,2pi);

real f(real x, real y) {return cos(x)*sin(y);}

int N=200;
int Divs=10;
int divs=1;
int n=Divs*divs;

defaultpen(1bp);
pen Tickpen=black;
pen tickpen=gray+0.5*linewidth(currentpen);
pen[] Palette=quantize(BWRainbow(),n);

bounds range=image(f,Automatic,a,b,3N,Palette,n);

// Major contours
real[] Cvals=uniform(range.min,range.max,Divs);
draw(contour(f,a,b,Cvals,N,operator --),Tickpen+squarecap+beveljoin);

// Minor contours (if divs > 1)
real[] cvals;
for(int i=0; i < Cvals.length-1; ++i)
  cvals.append(uniform(Cvals[i],Cvals[i+1],divs)[1:divs]);
draw(contour(f,a,b,cvals,N,operator --),tickpen);

xaxis("$x$",BottomTop,LeftTicks,above=true);
yaxis("$y$",LeftRight,RightTicks,above=true);

palette("$f(x,y)$",range,point(SE)+(0.5,0),point(NE)+(1,0),Right,Palette,
        PaletteTicks("$%+#0.1f$",N=Divs,n=divs,Tickpen,tickpen));

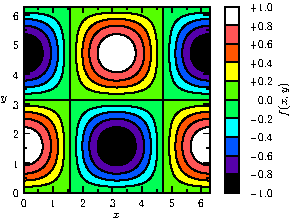
import graph;
import palette;
import contour;

size(10cm,10cm);

pair a=(0,0);
pair b=(2pi,2pi);

real f(real x, real y) {return cos(x)*sin(y);}

int N=200;
int Divs=10;
int divs=1;

defaultpen(1bp);
pen Tickpen=black;
pen tickpen=gray+0.5*linewidth(currentpen);
pen[] Palette=BWRainbow();

bounds range=image(f,Automatic,a,b,N,Palette);

// Major contours
real[] Cvals=uniform(range.min,range.max,Divs);
draw(contour(f,a,b,Cvals,N,operator --),Tickpen+squarecap+beveljoin);

// Minor contours (if divs > 1)
real[] cvals;
for(int i=0; i < Cvals.length-1; ++i)
  cvals.append(uniform(Cvals[i],Cvals[i+1],divs)[1:divs]);
draw(contour(f,a,b,cvals,N,operator --),tickpen+squarecap+beveljoin);

xaxis("$x$",BottomTop,LeftTicks,above=true);
yaxis("$y$",LeftRight,RightTicks,above=true);

palette("$f(x,y)$",range,point(SE)+(0.5,0),point(NE)+(1,0),Right,Palette,
        PaletteTicks("$%+#0.1f$",N=Divs,n=divs,Tickpen,tickpen));

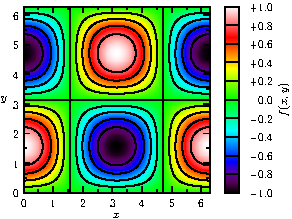
Finally, here is an example that illustrates the construction of contours from irregularly spaced data:

import contour;

size(200);

int n=100;

real f(real a, real b) {return a^2+b^2;}

srand(1);

real r() {return 1.1*(rand()/randMax*2-1);}

pair[] points=new pair[n];
real[] values=new real[n];

for(int i=0; i < n; ++i) {
  points[i]=(r(),r());
  values[i]=f(points[i].x,points[i].y);
}

draw(contour(points,values,new real[]{0.25,0.5,1},operator ..),blue);

In the above example, the contours of irregularly spaced data are constructed by first creating a triangular mesh from an array z of pairs:

int[][] triangulate(pair[] z);

size(200);
int np=100;
pair[] points;

real r() {return 1.2*(rand()/randMax*2-1);}

for(int i=0; i < np; ++i)
  points.push((r(),r()));

int[][] trn=triangulate(points);

for(int i=0; i < trn.length; ++i) {
  draw(points[trn[i][0]]--points[trn[i][1]]);
  draw(points[trn[i][1]]--points[trn[i][2]]);
  draw(points[trn[i][2]]--points[trn[i][0]]);
}

for(int i=0; i < np; ++i)
  dot(points[i],red);

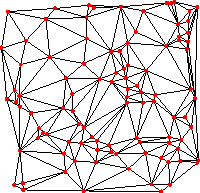
The example Gouraudcontour.asy illustrates how to produce color density images over such irregular triangular meshes. Asymptote uses a robust version of Paul Bourke’s Delaunay triangulation algorithm based on the public-domain exact arithmetic predicates written by Jonathan Shewchuk.