---

8.31 graph3 ¶

This module implements three-dimensional versions of the functions in graph.asy. To draw an x axis in three dimensions, use the routine

void xaxis3(picture pic=currentpicture, Label L="", axis axis=YZZero,
            real xmin=-infinity, real xmax=infinity, pen p=currentpen,
            ticks3 ticks=NoTicks3, arrowbar3 arrow=None,
            margin3 margin=NoMargin3, bool above=false,
            projection P=currentprojection);

Analogous routines yaxis and zaxis can be used to draw y and z axes in three dimensions. There is also a routine for drawing all three axis:

void axes3(picture pic=currentpicture,
           Label xlabel="", Label ylabel="", Label zlabel="",
           bool extend=false,
           triple min=(-infinity,-infinity,-infinity),
           triple max=(infinity,infinity,infinity),
           pen p=currentpen, arrowbar3 arrow=None,
           margin3 margin=NoMargin3, projection P=currentprojection);

The predefined three-dimensional axis types are

axis YZEquals(real y, real z, triple align=O, bool extend=false);
axis XZEquals(real x, real z, triple align=O, bool extend=false);
axis XYEquals(real x, real y, triple align=O, bool extend=false);
axis YZZero(triple align=O, bool extend=false);
axis XZZero(triple align=O, bool extend=false);
axis XYZero(triple align=O, bool extend=false);
axis Bounds(int type=Both, int type2=Both, triple align=O, bool extend=false);

The optional align parameter to these routines can be used to specify the default axis and tick label alignments. The Bounds axis accepts two type parameters, each of which must be one of Min, Max, or Both. These parameters specify which of the four possible three-dimensional bounding box edges should be drawn.

The three-dimensional tick options are NoTicks3, InTicks, OutTicks, and InOutTicks. These specify the tick directions for the Bounds axis type; other axis types inherit the direction that would be used for the Bounds(Min,Min) axis.

Here is an example of a helix and bounding box axes with ticks and axis labels, using orthographic projection:

import graph3;

size(0,200);
size3(200,IgnoreAspect);

currentprojection=orthographic(4,6,3);

real x(real t) {return cos(2pi*t);}
real y(real t) {return sin(2pi*t);}
real z(real t) {return t;}

path3 p=graph(x,y,z,0,2.7,operator ..);

draw(p,Arrow3);

scale(true);

xaxis3(XZ()*"$x$",Bounds,red,InTicks(Label,2,2));
yaxis3(YZ()*"$y$",Bounds,red,InTicks(beginlabel=false,Label,2,2));
zaxis3(XZ()*"$z$",Bounds,red,InTicks);

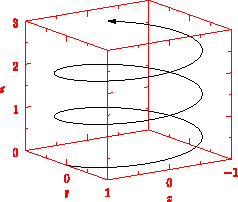
The next example illustrates three-dimensional x, y, and z axes, without autoscaling of the axis limits:

import graph3;

size(0,200);
size3(200,IgnoreAspect);

currentprojection=perspective(dir(75,20));

scale(Linear,Linear,Log);

xaxis3("$x$",0,1,red,OutTicks(2,2));
yaxis3("$y$",0,1,red,OutTicks(2,2));
zaxis3("$z$",1,30,red,OutTicks(beginlabel=false));

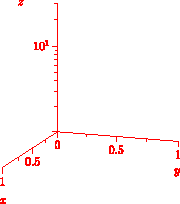
One can also place ticks along a general three-dimensional axis:

import graph3;

size(0,100);

path3 g=yscale3(2)*unitcircle3;
currentprojection=perspective(10,10,10);

axis(Label("C",position=0,align=15X),g,InTicks(endlabel=false,8,end=false),
     ticklocate(0,360,new real(real v) {
         path3 h=O--max(abs(max(g)),abs(min(g)))*dir(90,v);
         return intersect(g,h)[0];},
       new triple(real t) {return cross(dir(g,t),Z);}));

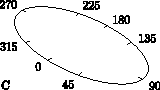
Surface plots of matrices and functions over the region box(a,b) in the XY plane are also implemented:

surface surface(real[][] f, pair a, pair b, bool[][] cond={});
surface surface(real[][] f, pair a, pair b, splinetype xsplinetype,
                splinetype ysplinetype=xsplinetype, bool[][] cond={});
surface surface(real[][] f, real[] x, real[] y,
                splinetype xsplinetype=null, splinetype ysplinetype=xsplinetype,
                bool[][] cond={})
surface surface(triple[][] f, bool[][] cond={});
surface surface(real f(pair z), pair a, pair b, int nx=nmesh, int ny=nx,
                bool cond(pair z)=null);
surface surface(real f(pair z), pair a, pair b, int nx=nmesh, int ny=nx,
                splinetype xsplinetype, splinetype ysplinetype=xsplinetype,
                bool cond(pair z)=null);
surface surface(triple f(pair z), real[] u, real[] v,
                splinetype[] usplinetype, splinetype[] vsplinetype=Spline,
                bool cond(pair z)=null);
surface surface(triple f(pair z), pair a, pair b, int nu=nmesh, int nv=nu,
                bool cond(pair z)=null);
surface surface(triple f(pair z), pair a, pair b, int nu=nmesh, int nv=nu,
                splinetype[] usplinetype, splinetype[] vsplinetype=Spline,
                bool cond(pair z)=null);

The final two versions draw parametric surfaces for a function f(u,v) over the parameter space box(a,b), as illustrated in the example parametricsurface.asy. An optional splinetype Spline may be specified. The boolean array or function cond can be used to control which surface mesh cells are actually drawn (by default all mesh cells over box(a,b) are drawn).

One can also construct the surface generated by rotating a path g between angle1 to angle2 (in degrees) sampled n times about the line c--c+axis:

surface surface(triple c, path3 g, triple axis, int n=nslice,
                real angle1=0, real angle2=360, pen color(int i, real j)=null);

The optional argument color(int i, real j) can be used to override the surface color at the point obtained by rotating vertex i by angle j (in degrees).

Surface lighting is illustrated in the example files parametricsurface.asy and sinc.asy. Lighting can be disabled by setting light=nolight, as in this example of a Gaussian surface:

import graph3;

size(200,0);

currentprojection=perspective(10,8,4);

real f(pair z) {return 0.5+exp(-abs(z)^2);}

draw((-1,-1,0)--(1,-1,0)--(1,1,0)--(-1,1,0)--cycle);

draw(arc(0.12Z,0.2,90,60,90,25),ArcArrow3);

surface s=surface(f,(-1,-1),(1,1),nx=5,Spline);

xaxis3(Label("$x$"),red,Arrow3);
yaxis3(Label("$y$"),red,Arrow3);
zaxis3(XYZero(extend=true),red,Arrow3);

draw(s,lightgray,meshpen=black+thick(),nolight,render(merge=true));

label("$O$",O,-Z+Y,red);

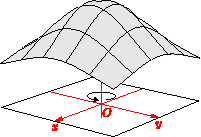
A mesh can be drawn without surface filling by specifying nullpen for the surfacepen.

A vector field of nu\timesnv arrows on a parametric surface f over box(a,b) can be drawn with the routine

picture vectorfield(path3 vector(pair v), triple f(pair z), pair a, pair b,
                    int nu=nmesh, int nv=nu, bool truesize=false,
                    real maxlength=truesize ? 0 : maxlength(f,a,b,nu,nv),
                    bool cond(pair z)=null, pen p=currentpen,
                    arrowbar3 arrow=Arrow3, margin3 margin=PenMargin3)

as illustrated in the examples vectorfield3.asy and vectorfieldsphere.asy.